协同过滤算法是最原始的推荐算法,即使在深度学习占据主场的今天,依旧有非常强的学习意义
User CF
相似的用户会喜欢相同的Item
优点:UserCF基于用户相似度推荐,非常具有社交特性,比较适合新闻场景
缺点:互联网场景中,用户数远大于Item数
-
用户相似度矩阵的存储开销非常大,用户数的增长会导致用户相似度矩阵的空间复杂度以的速度增长
-
用户历史数据非常稀疏,对于只有几次购买行为的用户,要找到与他相似的用户准确度非常低,导致
UserCF不适合正反馈获取困难的场景(酒店预订、大件商品购买等低频场景)
Item CF
获取m个用户和n个Item交互的矩阵,按照列计算不同Item之间的相似性,得到的相似度矩阵。针对用户正反馈中的Item,找到Top k个相似的Item,生成推荐列表.
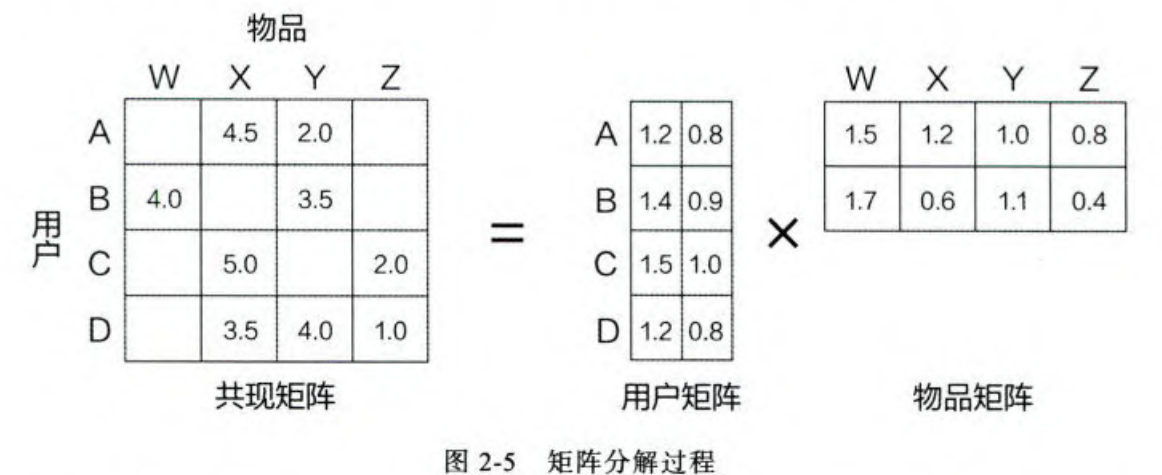
矩阵分解
CF的一个严重的缺点:热点Item有非常强的头部效应,导致和大量Item产生相似性,而尾部Item由于特征向量稀疏,很少和其他Item产生相似性,导致很少被推荐。
归根结底,不同Item的向量的稀疏性导致了推荐的缺陷,矩阵分解通过更加稠密的隐向量来挖掘用户和Item的隐含兴趣和隐含特征
的取值越小,隐向量包含的信息越少,模型的泛化程度越高;
的取值越大,隐向量的表达能力越强,但泛化程度相应降低。
此外, 的取值还与矩阵分解的求解复杂度直接相关。
在具体应用中, 的取值要经过多次试验找到一个推荐效果和工程开销的平衡点。
矩阵分解过程
-
特征值分解
-
奇异值分解(SVD)
-
梯度下降
特征值分解
只适合方阵来分解,User-Item矩阵可不是方阵,pass
奇异值分解
, 其中和是正交矩阵,的对角阵
-
奇异值分解要求原始共现矩阵是稠密的,但是互联网场景中,大部分用户的行为历史非常少,导致User-Item矩阵是稀疏的。
-
奇异值分解的时间复杂度为 ,这是不可接受的
梯度下降法
我们用表示用户的特征向量,表示的特征向量,那么用户和的相关性就是
那么训练损失就是:
这里的是来自共现矩阵中用户对Item的真实评价标签, 后面部分是正则化项。
优点:
-
泛化能力强:在一定程度上解决了数据稀疏问题。
-
更好的扩展性和灵活性:矩阵分解的最终产岀是用户和物品隐向量,这其实与深度学习中的 Embedding 思想不谋而合(不能说一样,只能说基本不差)
缺点:
- 还是不能加入用户(Age、gender)、Item(价格、评分、分类)和上下文的特征,损失了不少有用的信息