主要思想:
用户的兴趣是多样化的,而当前用户的兴趣仅与部分历史行为相关。
DIN通过注意力机制来衡量用户历史中每个物品与目标物品的相关性。相关性高的历史行为会获得更高的权重,而不相关的历史行为则可以被忽略。
原理
具体来说,模型接收三类输入:用户特征(如年龄、性别等)、用户历史行为(曾经点击过的item)以及目标Item的特征(商品信息)。
以下是一个示例,假设有用户(u)和目标物品(i):
-
用户(u)的特征可能是 ([age:25,gender:male,location:Shanghai])
-
用户(u)的历史行为序列可能是 ([item1,item2,item3])
-
目标物品(i)的特征可能是 ([category:electronics,brand:Samsung,price:5000])
-
如果用户(u)点击了物品(i),标签为1;未点击则为0
首先,系统将所有特征转换为稠密嵌入向量。
注意力机制
通过注意力机制,系统计算每个历史行为与目标item的相关性。用户历史行为序列[item1, item2, item3]中的每个元素都代表一次用户行为,每个行为都转换为嵌入向量[e1,e2,e3],然后计算每个ei与目标Itemi的相关性分数。将这些相关性分数与原始历史行为embedding相乘并求和,得到用户兴趣表示v∗U(A)。
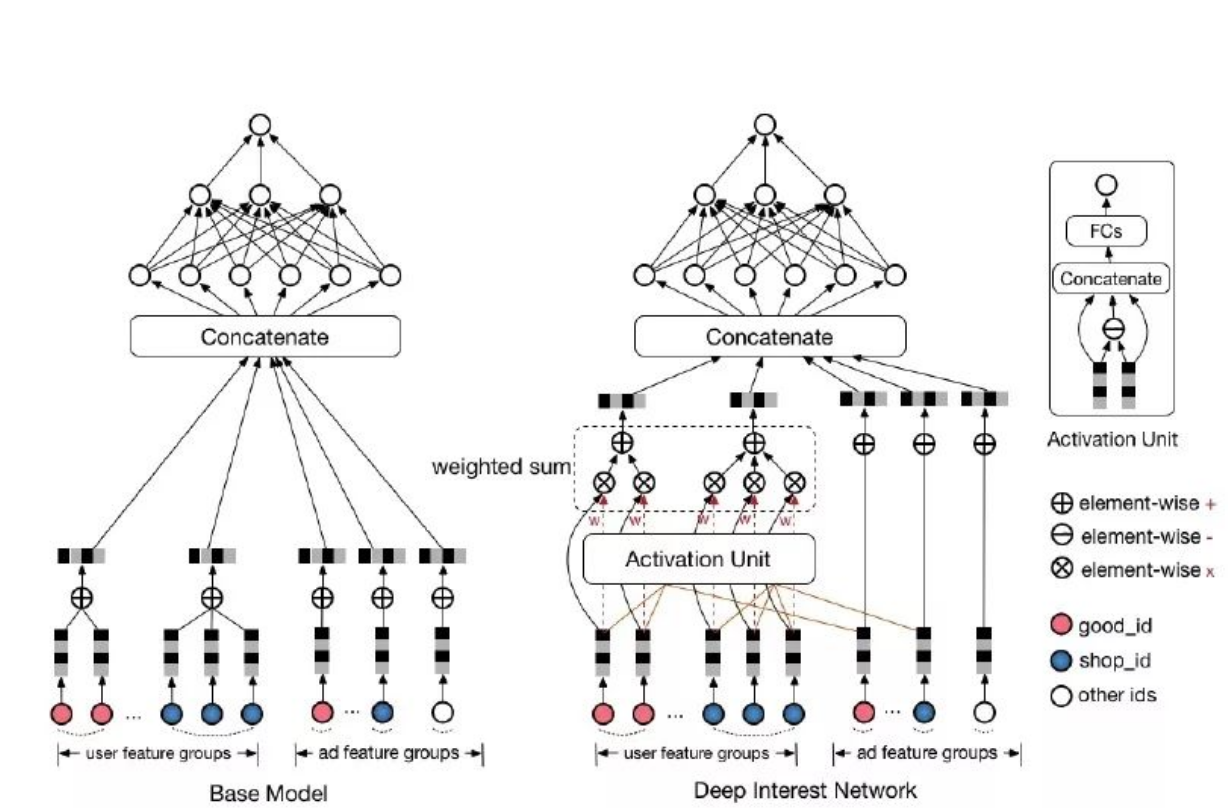
计算公式如下:v∗U(A)=f(vA,e1,e2,…,eH)=∑j=1Ha(ej,vA)ej。
其中e1,e2,…,eH是用户U的历史行为特征embedding,vA 表示候选广告A的embedding向量,a(ej,vA)=wj表示历史行为商品与当前广告A的相关性程度。a(⋅)代表前馈神经网络,即注意力机制。
值得注意的是,输入除了包含历史行为向量和候选广告向量外,还包括它们的外积操作,这有助于模型进行显式的相关性建模。
需要特别说明的是,这里的权重之和不是1。准确地说,这里使用的不是标准化权重,而是直接使用相关性分数作为权重(即softmax之前的scores值),这样可以保留用户兴趣的强度信息。
另外需要注意的是,这种历史行为具有序列性质,且不同用户的历史行为特征长度可能不同。由于神经网络要求序列等长,我们通常会通过padding操作(用0填充)使序列达到最长长度。在具体计算时,使用mask掩码来标记填充位置,以确保计算准确性。
Dice
公式:
dice(X)=p(X)⋅X+(1−p(X))⋅αX(其中,p(X)=1+exp(−Var(X)+ϵX−E(X))1)=sigmoid(BN(X))⋅X+(1−sigmoid(BN(X)))⋅αX
就是在BN的基础上继续做了变换。
初始化模型参数
这是深度学习模型普遍面临的问题。通常通过Xavier初始化或He初始化来缓解梯度消失或爆炸问题。
-
Xavier初始化:从N(0,σ)分布中采样权重矩阵,其中σ=2nin+nout
-
He初始化:为缓解ReLU的梯度消失问题而提出,从N(0,σ)分布中采样权重矩阵,其中σ=2nin,nin表示矩阵的输入节点数。由于ReLU在小值区域容易产生零梯度,因此通过增大权重标准差来缓解这一问题。
冷启动
解决方案是先使用基于内容的推荐或规则based推荐,待累积足够数据量后再切换到DIN。
数据不平衡问题
在搜索广告推荐领域,用户点击物品通常表示确实感兴趣,但未点击并不一定代表不感兴趣——可能只是漏看了。在收集的数据中,正样本(感兴趣)往往远少于负样本(不感兴趣)。解决方案包括:过采样/欠采样,或在损失函数中对多数类样本施加较小权重,对少数类样本施加较大权重。
