常见位置编码及其实现

可学习位置编码

可学习位置编码是指将位置编码作为一种可学习的参数直接加入到词嵌入向量中。这种方法操作简单，容易理解，所有词的位置信息全靠模型自己学习。

由于可学习位置编码矩阵是固定的，所以模型在推理的时候并没有外推性，遇到超过训练长度的长文本会无法推理。

大模型外推性（Length Extrapolation）

外推性是指大模型在训练时和预测时的输入长度不一致，导致模型的泛化能力下降的问题。

例如，如果一个模型在训练时只使用了512个 token 的文本，那么在预测时如果输入超过512个 token，模型可能无法正确处理。这就限制了大模型在处理长文本或多轮对话等任务时的效果。

正余弦位置编码

三角函数位置信息编码无需训练，提供了绝对位置信息和一定程度的外推性。

正余弦位置编码公式如下：

$$PE(pos, 2i) = \sin(\frac{pos}{10000^{2i /d_{model}}})\\ PE(pos, 2i + 1) = \cos(\frac{pos}{10000^{2i / d_{model}}})$$

在同一个位置pos中，不同维度的正余弦值不同。$\frac{2i}{d_{model}}$是为了做归一化，在低维度（i较小）中，公式的分母较小，频率更高，因此更加关注局部的位置变化；在高维度（i较大）中，频率更低，因此更加关注全局的位置变化。

在外推时，如果遇到更长的位置，可以根据三角变换公式$sin(a + b) = sin(a) cos(b) + cos(a) sin(b)$, 推导出任意位置的位置嵌入向量。

正余弦位置编码在外推性上的局限性：

只要Attention向量计算结果中能够表征出位置之差$m - n$，那就是有相对位置表征能力。

在正余弦位置编码中，位置$i$上的词$word_i$和位置$i + k$上的词$word_{i +k}$之间做QK计算：

$$\begin{align} q^T_{word_1}k_{word_{2}} & = ((embed_{1} + PE_1) W_q )^T \cdot ((embed_2 + PE_2) W_k )\\ & = W_q^T (embed_1 + PE_1)^T (embed_2 + PE_2) W_k\\ & = W_q^T (embed_1^T embed_2 + embed_1^T PE_2 + embed_2^T PE_1 + PE_1^T PE_2) W_k \end{align}$$

继续分析$PE_2$和$PE_1$ :

$$\begin{align} PE(pos + k, 2i ) & = sin ((pos + k) / (10000^{2i /dmodel})) \\ & = sin(pos / (10000^{2i /dmodel}) ) cos(k / (10000^{2i /dmodel})) + cos(pos / (10000^{2i /dmodel}) ) sin(k / (10000^{2i /dmodel})) \\ & = PE(pos, 2i) u + PE(pos, 2i + 1) v \end{align}$$

同理， $PE(pos + k , 2i + 1) = u PE(pos, 2i + 1) - v PE(pos, 2i)$

那么:

$$PE_1^T PE_2 = 2u = 2 cos(k / 10000^{2i / dmodel}) (严谨来说，这里应该是求和)$$

因此，$q_{word_1}^T k_{word_2}$的公式内部是存在一部分$cos(k / 10000^{2i / dmodel})$，能够表征出$k$, 所以具有一定程度上的相对位置表征能力。

随着$k$增大，余弦函数是渐渐变小的，这就意味着两个Token之间越远，Token之间的相关程度越弱，这种远程衰减便是相对位置表征能力不足的原因

Rotary旋转位置编码

RoPE相比正余弦位置编码提供了更加自然的相对位置表示，相对位置是指在计算Attention的时候考虑当前位置与被Attention的位置的相对距离。

在正余弦位置编码中，词向量和位置向量相加之后的向量送入Attention中计算，在一定程度上也能引入相对位置信息，只不过不够明显。

ROPE中将通过独特设计的词向量和query相乘，等价出来一个相对位置操作，因此是显式引入相对位置。

优点：

• 可以扩展到任意序列长度

• 随着相对距离的增加，token之间的依赖性减弱

• 为线性自注意力配备相对位置编码的能力

我们假设已经找到了一个非常优美良好的函数$f(q, i)$可以提供不同位置的位置向量，$q$是词向量，$i$是这个词所在的位置。现在计算该词和另外一个词的Attention，已知两个词之间的距离为$m - n$, 我们期望$Attention(word_m, word_n) = f(q_m, m) * f(q_n, n) = g(q_m, q_n, m - n)$, 现在问题就是哪里找到能够满足条件的函数 $f$ 和 $g$ .

在复数空间中，我们知道

$$z \cdot e^{i \theta} = (a + b i) (cos(\theta) + i \cdot sin(\theta)) = (a \cdot cos(\theta) - b \cdot sin(\theta)) + i \cdot(a \cdot sin(\theta) + b \cdot cos(\theta)) = R(\theta) \cdot z \\ R(\theta) = \left[ \begin{matrix} cos(\theta) & - sin(\theta) \\\\ sin(\theta) & cos(\theta) \end{matrix} \right]$$

那么可以推导出：

$$(R(\theta_1) z_1)^T \cdot (R(\theta_2) z_2) = z_1^T R(\theta_1)^T R(\theta_2) z_2 = z_1^T R(\theta_1 - \theta_2) z_2$$

正好可以发现满足要求的$f$和$g$, 其中$f = R(\theta) z$, $g = (z_1, z_2, \theta_1 - \theta_2)$

ROPE根据上面找到的 $f$ 和 $g$ , 将词向量视作一个复数向量，并对每一个维度进行旋转操作, 旋转角度$\theta = pos / 10000^{2i /d_{model}}$ , 那么在进行Attention计算的时候，就自动引入了相对位置，因为根据上述公式，Attention的计算过程等价成了$g$函数，$g$函数是显式引入了相对位置操作$m - n$ .

ROPE 线性插值

虽然ROPE在公式上具有比较良好的相对位置表征能力，但是在外推的时候依然会有性能下降的问题。例如模型在2048的context窗口中训练，但是推理时候遇到5096长度的context窗口，就会性能下降。

一种解决方案便是进行线性插值，$L$为预训练的最大窗口长度，$L^{'}$为当前样本长度，那么$f^{`}(x, m) = f(x, \frac{m L}{L^{`}})$ ，如下图所示

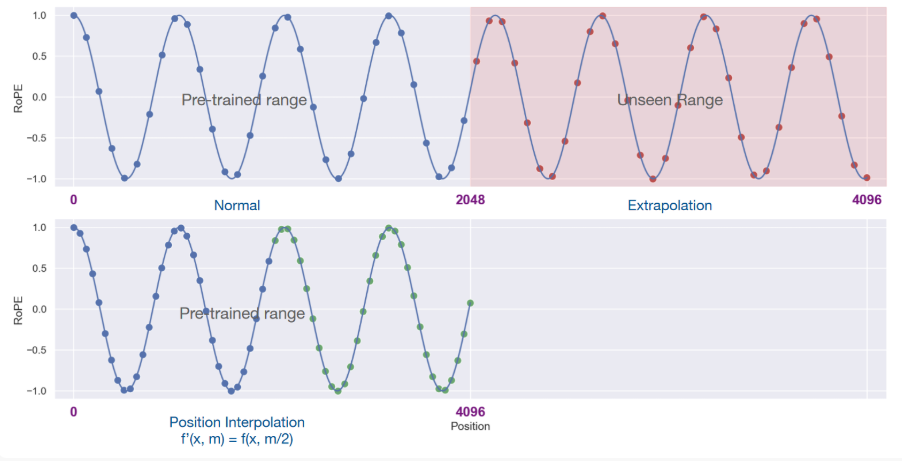
线性插值会导致ROPE的旋转角度变小，例如原来两个Token之间的距离为$k$，两个Token之间旋转角度之差为$\theta_1$, 但是由于线性插值导致旋转角度变小，因此现在距离为$k$的两个Token之间的角度之差也就变小了，也就导致局部信息的相关性降低。总结如下：

• 位置插值会缩小旋转弧度

• 降低旋转速度

• 导致模型的高频信息缺失，从而影响模型的性能。

ROPE 非线性插值方案（NTK-Aware scaled ROPE）

非线性插值的思路是修改ROPE的Base值，也就是那个10000.

那为什么非线性插值更好呢？挖坑待填，我也不知道

Alibi （Attention linear bias）

Alibi同样是不直接在词向量上加位置嵌入表示，而是通过在Attention的机制上修改，加上相对位置信息。

Attention的计算是$q_{token_i}^T k_{token_j}$, 那么直接在计算中补上相对位置信息：$q_{token_i}^T k_{token_j} + (pos_{token_i} - pos_{token_j})$ ，大道至简，简洁明了。

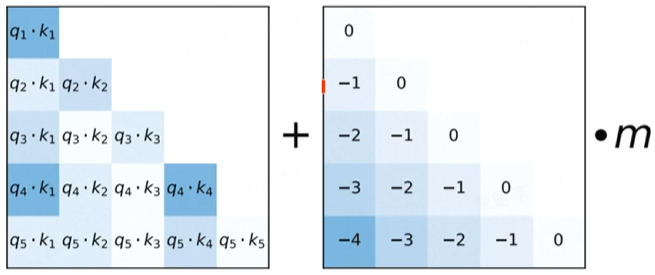
Attention的多头实现中，还可以为不同的head分配不同的系数，实现多样化的相对位置信息表征。

代码实现

import math

import torch

import torch.nn as nn



class PositionEncoding(nn.Module):

    def __init__(self, embed_dim, max_len=5000, strategy="sinusoidal"):

        """

        支持多种位置编码策略

        :param embed_dim: 嵌入维度

        :param max_len: 最大序列长度

        :param strategy: 位置编码策略 ("sinusoidal", "learnable", "rope")

        """

        super().__init__()

        self.strategy = strategy

        self.embed_dim = embed_dim



        if strategy == "sinusoidal":

            self.position_encoding = self._create_sinusoidal_encoding(embed_dim, max_len)

        elif strategy == "learnable":

            self.position_encoding = nn.Parameter(torch.zeros(max_len, embed_dim))

            nn.init.normal_(self.position_encoding, mean=0, std=0.02)

        elif strategy == "rope":

            # ROPE 不直接存储编码，而是动态计算旋转

            self.inv_freq = 1.0 / (10000 ** (torch.arange(0, embed_dim, 2).float() / embed_dim))

        else:

            raise ValueError(f"Unknown position encoding strategy: {strategy}")



    def _create_sinusoidal_encoding(self, embed_dim, max_len):

        position = torch.arange(max_len).unsqueeze(1) # [max_len, 1]

        div_term = torch.exp(torch.arange(0, embed_dim, 2) * (-math.log(10000.0) / embed_dim))

        pe = torch.zeros(max_len, embed_dim)

        pe[:, 0::2] = torch.sin(position * div_term)

        pe[:, 1::2] = torch.cos(position * div_term)

        return pe



    def forward(self, x):

        """

        根据策略应用位置编码

        :param x: 输入张量，形状 [batch_size, seq_len, embed_dim]

        """

        if self.strategy == "sinusoidal":

            return x + self.position_encoding[:x.size(1), :].to(x.device)

        elif self.strategy == "learnable":

            return x + self.position_encoding[:x.size(1), :].to(x.device)

        elif self.strategy == "rope":

            return self._apply_rope(x)

        else:

            raise ValueError(f"Unknown position encoding strategy: {self.strategy}")



    def _apply_rope(self, x):

        """

        应用 ROPE 编码

        """

        batch_size, seq_len, _ = x.size()

        pos_seq = torch.arange(seq_len, device=x.device).unsqueeze(1)

        sin, cos = torch.sin(pos_seq * self.inv_freq), torch.cos(pos_seq * self.inv_freq)

        sin_cos = torch.stack((sin, cos), dim=-1).reshape(seq_len, -1)  # [seq_len, embed_dim]

        x_even, x_odd = x[..., 0::2], x[..., 1::2]

        return torch.cat((x_even * cos - x_odd * sin, x_even * sin + x_odd * cos), dim=-1)